
The Cg Tutorial
The Cg Tutorial is now available, right here, online. You can purchase a beautifully printed version of this book, and others in the series, at a 30% discount courtesy of InformIT and Addison-Wesley.Please visit our Recent Documents page to see all the latest whitepapers and conference presentations that can help you with your projects.
Chapter 3. Parameters, Textures, and Expressions
This chapter continues to present Cg concepts through a series of simple vertex and fragment programs. The chapter has the following three sections:
- "Parameters" explains how Cg programs handle parameters.
- "Texture Samplers" explains how fragment programs access textures.
- "Math Expressions" shows how math expressions compute new vertex and fragment values.
3.1 Parameters
The C2E1v_green and C2E2f_passthrough examples from Chapter 2 are very basic. We will now broaden these examples to introduce additional parameters.
3.1.1 Uniform Parameters
C2E1v_green (see page 38 in Chapter 2) always assigns green for the vertex color. If you rename the C2E1v_green program and change the line that assigns the value of OUT.color , you can potentially make a different vertex program for any color you like.
For example, changing the appropriate line results in a hot pink shader:
OUT.color = float4(1.0, 0.41, 0.70, 1.0); // RGBA hot pink
The world is a colorful place, so you wouldn't want to have to write a different Cg program for every color under the sun. Instead, you can generalize the program by passing it a parameter that indicates the currently requested color.
The C3E1v_anyColor vertex program in Example 3-1 provides a constantColor parameter that your application can assign to any color, rather than just a particular constant color.
Example 3-1. The C3E1v_anyColor Vertex Program
struct C3E1v_Output {
float4 position : POSITION;
float4 color : COLOR;
};
C3E1v_Output C3E1v_anyColor(float2 position : POSITION,
uniform float4 constantColor)
{
C3E1v_Output OUT;
OUT.position = float4(position, 0, 1);
OUT.color = constantColor; // Some RGBA color
return OUT;
}
The difference between C3E1v_anyColor and C2E1v_green is the function interface definition and what each program assigns to OUT.color .
The updated function definition is this:
C3E1v_Output C3E1v_anyColor(float2 position : POSITION,
uniform float4 constantColor)
In addition to the position parameter, the new function definition has a parameter named constantColor that the program defines as type uniform float4 . As we discussed earlier, the float4 type is a vector of four floating-point values—in this case, assumed to be an RGBA color. What we have not discussed is the uniform type qualifier.
The uniform Type Qualifier
The uniform qualifier indicates the source of a variable's initial value. When a Cg program declares a variable as uniform , it conveys that the variable's initial value comes from an environment that is external to the specified Cg program. This external environment contains your 3D programming interface state and other name/value pairs established through the Cg runtime.
In the case of the constantColor variable in the C3E1v_anyColor example, the Cg compiler generates a vertex program that retrieves the variable's initial value from a vertex processor constant register within the GPU.
Using the Cg runtime, your 3D application can query a parameter handle for a uniform parameter name within a Cg program—in this case, constantColor —and use the handle to load the proper value for the particular uniform variable into the GPU. The details of how uniform parameter values are specified and loaded vary by profile, but the Cg runtime makes this process easy. Appendix B explains how to do this.
Our C3E1v_anyColor vertex program assigns the vertex output color to the value of its constantColor uniform variable, as shown:
OUT.color = constantColor; // Some RGBA color
Whatever color the application specifies for the constantColor uniform variable is the color that the Cg program assigns to the output vertex color when C3E1v_anyColor transforms a vertex.
The addition of a uniform parameter lets us generalize our initial example to render any color, when originally it could render only green.
When There Is No uniform Qualifier
When a Cg program does not include the uniform qualifier to specify a variable, you can assign the initial value for the variable in one of the following ways:
- Using an explicit initial assignment:
float4 green = float4 (0, 1, 0, 1); - Using a semantic:
float4 position : POSITION; -
Leaving it undefined or equal to zero, depending on the profile:
float whatever; // May be initially undefined or zero
What uniform Means in RenderMan vs. Cg
In RenderMan, the uniform storage modifier indicates variables whose values are constant over a shaded surface, whereas varying variables are those whose values can vary over the surface.
Cg does not have this same distinction. In Cg, a uniform -qualified variable obtains its initial value from an external environment and, except for this initialization difference, is the same as any other variable. Cg permits all variables to vary, unless the variable has the const type qualifier specified. Unlike RenderMan, Cg has no varying reserved word.
Despite the semantic difference between RenderMan's concept of uniform and Cg's concept of it, variables declared uniform in RenderMan correspond to variables declared uniform in Cg, and vice versa.
3.1.2 The const Type Qualifier
Cg also provides the const qualifier. The const qualifier affects variables the same way that the const qualifier does in C and C++: it restricts how a variable in your program may be used. You cannot assign a value to, or otherwise change, a variable that is specified as constant. Use the const qualifier to indicate that a certain value should never change. The Cg compiler will generate an error if it detects usage that would modify a variable declared as const .
Here are some examples of usage not allowed when a program qualifies a variable with const :
const float pi = 3.14159; pi = 0.4; // An error because pi is specified const float a = pi++; // Implicit modification is also an error
The const and uniform type qualifiers are independent, so a variable can be specified using const or uniform , both const and uniform , or neither.
3.1.3 Varying Parameters
You have already seen examples of a per-vertex varying parameter in both C2E1v_green and C3E1v_anyColor . The POSITION input semantic that follows the position parameter in C2E1v_green and C3E1v_anyColor indicates that the GPU is to initialize each respective position parameter with the input position of each vertex processed by each respective program.
Semantics provide a way to initialize Cg program parameters with values that vary either from vertex to vertex (in vertex programs) or fragment to fragment (in fragment programs).
A slight modification to C3E1v_anyColor , called C3E2v_varying , in Example 3-2, lets the program output not merely a single constant color, but rather a color and texture coordinate set (used for accessing textures) that can vary per vertex.
Example 3-2. The C3E2v_varying Vertex Program
struct C3E2v_Output {
float4 position : POSITION;
float4 color : COLOR;
float2 texCoord : TEXCOORD0;
};
C3E2v_Output C3E2v_varying(float2 position : POSITION,
float4 color : COLOR,
float2 texCoord : TEXCOORD0)
{
C3E2v_Output OUT;
OUT.position = float4(position, 0, 1);
OUT.color = color;
OUT.texCoord = texCoord;
return OUT;
}
The C3E2v_varying example prototypes its vertex program as:
C3E2v_Output C3E2v_varying(float2 position : POSITION,
float4 color : COLOR,
float2 texCoord : TEXCOORD0)
The C3E2v_varying example replaces the constantColor parameter declared as a uniform parameter in the C3E1v_anyColor example with two new nonuniform parameters, color and texCoord . The program assigns the COLOR and TEXCOORD0 semantics, respectively, to the two parameters. These two semantics correspond to the application-specified vertex color and texture coordinate set zero, respectively.
Instead of outputting the per-vertex position and a constant color, this new program transforms each vertex by outputting each vertex's position, color, and a single texture coordinate set with the following code:
OUT.position = float4(position, 0, 1); OUT.color = color; OUT.texCoord = texCoord;
Figure 3-1 shows the result of rendering our original triangle using the C3E2v_varying vertex program and the C2E2f_passthrough fragment program. Here, we assume that you have used OpenGL or Direct3D to assign the vertices of the triangle the per-vertex colors bright blue for the top two vertices and off-blue for the bottom vertex. Color interpolation performed by the rasterization hardware smoothly shades the interior fragments of the triangle. Although per-vertex texture coordinates are input and output by the C3E2v_varying vertex program, the subsequent C2E2f_passthrough fragment program ignores the texture coordinates.

Figure 3-1 Rendering a Gradiated 2D Triangle with and
3.2 Texture Samplers
The C3E2v_varying example passed per-vertex texture coordinates through the vertex program. Although the C2E2f_passthrough fragment program ignores texture coordinates, this next fragment program, called C3E3f_texture and shown in Example 3-3, uses the texture coordinates to sample a texture image.
Example 3-3. The C3E3f_texture Fragment Program
struct C3E3f_Output {
float4 color : COLOR;
};
C3E3f_Output C3E3f_texture(float2 texCoord : TEXCOORD0,
uniform sampler2D decal)
{
C3E3f_Output OUT;
OUT.color = tex2D(decal, texCoord);
return OUT;
}
The C3E3f_Output structure is essentially the same as the C2E2f_Output structure used by C2E2f_passthrough , our prior fragment program example. What is new about the C3E3f_texture example is in its declaration:
C3E3f_Output C3E3f_texture(float2 texCoord : TEXCOORD0,
uniform sampler2D decal)
The C3E3f_texture fragment program receives an interpolated texture coordinate set but ignores the interpolated color. The program also receives a uniform parameter called decal of type sampler2D .
3.2.1 Sampler Objects
A sampler in Cg refers to an external object that Cg can sample, such as a texture. The 2D suffix for the sampler2D type indicates that the texture is a conventional two-dimensional texture. Table 3-1 lists other sampler types supported by Cg that correspond to different kinds of textures. You will encounter some of these in later chapters.
Table 3-1. Cg Sampler Types
|
Sampler Type |
Texture Type |
Applications |
|---|---|---|
|
sampler1D |
One-dimensional texture |
1D functions |
|
sampler2D |
Two-dimensional texture |
Decals, normal maps, gloss maps, shadow maps, and others |
|
sampler3D |
Three-dimensional texture |
Volumetric data, 3D attenuation functions |
|
samplerCUBE |
Cube map texture |
Environment maps, normalization cube maps |
|
samplerRECT |
Non-power-of-two, non-mipmapped 2D texture |
Video images, photographs, temporary buffers |
Texture coordinates specify where to look when accessing a texture. Figure 3-2 shows a 2D texture, along with a query based on the texture coordinates (0.6, 0.4). Typically, texture coordinates range from 0 to 1, but you can also use values outside the range. We will not go into detail about this here, because the resulting behavior depends on how you set up your texture in OpenGL or Direct3D.
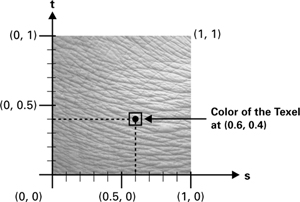
Figure 3-2 Querying a Texture
The semantic for the texture coordinate set named texCoord in Example 3-3 is TEXCOORD0 , corresponding to the texture coordinate set for texture unit 0. As the name of the sampler parameter decal implies, the intent of this fragment program is to use the fragment's interpolated texture coordinate set to access a texture.
3.2.2 Sampling Textures
The next interesting line of C3E3f_texture accesses the decal texture with the interpolated texture coordinates:
OUT.color = tex2D(decal, texCoord);
The routine tex2D belongs to the Cg Standard Library. It is a member of a family of routines that access different types of samplers with a specified texture coordinate set and then return a vector result. The result is the sampled data at the location indicated by the texture coordinate set in the sampler object.
In practice, this amounts to a texture lookup. How the texture is sampled and filtered depends on the texture type and texture parameters of the texture object associated with the Cg sampler variable. You can determine the texture properties for a given texture by using OpenGL or Direct3D texture specification commands, depending on your choice of 3D programming interface. Your application is likely to establish this association by using the Cg runtime.
The 2D suffix indicates that tex2D must sample a sampler object of type sampler2D . Likewise, the texCUBE routine returns a vector, accepts a sampler of type samplerCUBE for its first argument, and requires a three-component texture coordinate set for its second argument.
Basic fragment profiles (such as ps_1_1 and fp20 ) limit texture-sampling routines, such as tex2D and texCUBE , to the texture coordinate set that corresponds to the sampler's texture unit. To be as simple as possible and support all fragment profiles, the C3E3f_texture example follows this restriction. (See Section 2.3.1 for a brief introduction to profiles.)
Advanced fragment profiles (such as ps_2_x, arbfp1 , and fp30 ) allow a sampler to be sampled using texture coordinate sets from other texture units, or even texture coordinates computed in your Cg program.
3.2.3 Sending Texture Coordinates While Sampling a Texture
The C3E2v_varying vertex program passes a per-vertex position, color, and texture coordinate set to the rasterizer. The C3E3f_texture fragment program ignores the interpolated color, but samples a texture image with the interpolated texture coordinate set. Figure 3-3 shows what happens when you first bind both Cg programs with a texture that contains the image of a gruesome face, and then render our simple triangle with additional per-vertex texture coordinates assigned.

Figure 3-3 Rendering a Textured 2D Triangle with and
3.3 Math Expressions
So far, all the Cg examples we've presented have done little more than pass along parameters, or use a parameter to sample a texture. Conventional nonprogrammable 3D programming interfaces can accomplish just as much. The point of these examples was to introduce you to Cg and show the structure of simple Cg programs.
More interesting Cg programs perform computations on input parameters by using operators and built-in functions provided by the Cg Standard Library.
3.3.1 Operators
Cg supports the same arithmetic, relational, and other operators provided by C and C++. This means that addition is expressed with a + sign, multiplication with a * symbol, and greater-than-or-equal-to with the >= operator. You have already seen in prior examples that assignment is accomplished with the = sign.
Here are some examples of Cg expressions:
float total = 0.333 * (red + green + blue); total += 0.333 * alpha; float smaller = (a < b) ? a : b; float eitherOption = optionA || optionB; float allTrue = v[0] && v[1] && v[2];
Cg is different from C and C++ because it provides built-in support for arithmetic operations on vector quantities. You can accomplish this in C++ by writing your own classes that use operator overloading, but vector math operations are a standard part of the language in Cg.
The following operators work on vectors in a component-wise fashion:
| Operator | Name |
|---|---|
|
* |
Multiplication |
|
/ |
Division |
|
- |
Negation |
|
+ |
Addition |
|
- |
Subtraction |
When a scalar and a vector are used as operands of one of these component-wise operators, the scalar value is replicated (sometimes called "smeared") into a vector of the matching size.
Here are some examples of vector Cg expressions:
float3 modulatedColor = color * float3(0.2, 0.4, 0.5); modulatedColor *= 0.5; float3 specular = float3(0.1, 0.0, 0.2); modulatedColor += specular; negatedColor = -modulatedColor; float3 direction = positionA – positionB;
Table 3-2 presents the complete list of operators, along with their precedence, associativity, and usage. Operators marked with a reverse highlight are currently reserved. However, no existing Cg profiles support these reserved operators because current graphics hardware does not support bitwise integer operations.
Table 3-2. Precedence, Associativity, and Usage of Operators
|
Operators |
Associativity |
Usage |
|---|---|---|
|
( ) [ ] |
Left to right |
Function call, array reference, structure reference, component selection |
| ! ~ ++ - + - * & (type) sizeof |
Right to left |
Unary operators: negation, increment, decrement, positive, negative, indirection, address, cast |
| * / % |
Left to right |
Multiplication, division, remainder |
| + - |
Left to right |
Addition, subtraction |
| << >> |
Left to right |
Shift operators |
| < <= > >= |
Left to right |
Relational operators |
| == != |
Left to right |
Equality, inequality |
| & |
Left to right |
Bitwise AND |
| ^ |
Left to right |
Bitwise exclusive OR |
| | |
Left to right |
Bitwise OR |
| && |
Left to right |
Logical AND |
| || |
Left to right |
Logical OR |
| ? : |
Right to left |
Conditional expression |
| = += -= *= /= %= &= ^= |= <<= >>= |
Right to left |
Assignment, assignment expressions |
| , |
Left to right |
Comma operator |
|
Notes |
||
|
||
3.3.2 Profile-Dependent Numeric Data Types
When you program in C or C++ and declare variables, you pick from a few different-sized integer data types ( int , long , short , char ) and a couple of different-sized floating-point data types ( float , double ).
Your CPU provides the hardware support for all these basic data types. However, GPUs do not generally support so many data types—though, as GPUs evolve, they promise to provide more data types. For example, existing GPUs do not support pointer types in vertex or fragment programs.
Representing Continuous Data Types
Cg provides the float , half , and double floating-point types. Cg's approach to defining these types is similar to C's—the language does not mandate particular precisions. It is understood that half has a range and precision less than or equal to the range and precision of float , and float has a range and precision less than or equal to the range and precision of double .
The half data type does not exist in C or C++. This new data type introduced by Cg holds a half-precision floating-point value (typically 16-bit) that is more efficient in storage and performance than standard-precision floating-point (typically 32-bit) types.
GPUs, by design, provide data types that represent continuous quantities, such as colors and vectors. GPUs do not (currently) support data types that represent inherently discrete quantities, such as alphanumeric characters and bit masks, because GPUs do not typically operate on this kind of data.
Continuous quantities are not limited to integer values. When programming a CPU, programmers typically use floating-point data types to represent continuous values because floating-point types can represent fractional values. Continuous values processed by GPUs, particularly at the fragment level, have been limited to narrow ranges such as [0, 1] or [-1, +1], rather than supporting the expansive range provided by floating-point. For example, colors are often limited to the [0, 1] range, and normalized vectors are, by definition, confined to the [-1, +1] range. These range-limited data types are known as "fixed-point," rather than floating-point.
Although fixed-point data types use limited precision, they can represent continuous quantities. However, they lack the range of floating-point data types, whose encoding is similar to scientific notation. A floating-point value encodes a variable exponent in addition to a mantissa (similar to how numbers are written in scientific notation, such as 2.99 x 108), whereas a fixed-point value assumes a fixed exponent. For example, an unnormalized vector or a sufficiently large texture coordinate may require floating-point for the value to avoid overflowing a given fixed-point range.
Current GPUs handle floating-point equally well when executing vertex and fragment programs. However, earlier programmable GPUs provide floating-point data types only for vertex processing; they offer only fixed-point data types for fragment processing.
Cg must be able to manipulate fixed-point data types to support programmability for GPUs that lack floating-point fragment programmability. This means that certain fragment profiles use fixed-point values. Table 3-3 lists various Cg profiles and describes how they represent various data types. The implication for Cg programmers is that float may not actually mean floating-point in all profiles in all contexts.
Table 3-3. Data Types for Various Profiles
|
Profile Names |
Types |
Numerics |
|
arbfp1 arbvp1 vs_1_1 vs_2_0 vp20 vp30 |
float double half fixed |
Floating-point |
|
int |
Floating-point clamped to integers |
|
|
fp20 |
float double half int fixed |
Floating-point for texture mapping; fixed point with [-1, +1] range for fragment coloring |
|
ps_1_1 ps_1_2 ps_1_3 |
float double half int fixed |
Floating-point for texture mapping; fixed-point with GPU-dependent range for fragment coloring; range depends on underlying Direct3D capability |
|
ps_2_0 ps_2_x |
float double |
24-bit floating-point (minimum) |
|
int |
Floating-point clamped to integers |
|
|
half |
16-bit floating-point (minimum) |
|
|
fixed |
Depends on compiler settings |
|
|
fp30 |
float double |
Floating-point |
|
int |
Floating-point clamped to integers |
|
|
half |
16-bit floating-point |
|
|
fixed |
Fixed-point with [-2, 2) range |
3.3.3 Standard Library Built-In Functions
The Cg Standard Library contains many built-in functions that simplify GPU programming. In many cases, the functions map to a single native GPU instruction, so they can be very efficient.
These built-in functions are similar to C's Standard Library functions. The Cg Standard Library provides a practical set of trigonometric, exponential, vector, matrix, and texture functions. But there are no Cg Standard Library routines for input/output, string manipulation, or memory allocation, because Cg does not support these operations (though your C or C++ application certainly could).
We already used one Cg Standard Library function, tex2D , in Example 3-3. Refer to Table 3-4 for a select list of other functions that the Cg Standard Library provides. You can find a complete list of Cg Standard Library functions in Appendix E.
Table 3-4. Selected Cg Standard Library Functions
|
Function Prototype |
Profile Usage |
Description |
|
abs( x ) |
All |
Absolute value |
|
cos( x ) |
Vertex, advanced fragment |
Cosine of angle in radians |
|
cross( v1, v2 ) |
Vertex, advanced fragment |
Cross product of two vectors |
|
ddx( a ) ddy( a ) |
Advanced fragment |
Approximate partial derivatives of a with respect to window-space x or y coordinate, respectively |
|
determinant( M ) |
Vertex, advanced fragment |
Determinant of a matrix |
|
dot( a, b ) |
All, but restricted basic fragment |
Dot product of two vectors |
|
floor( x ) |
Vertex, advanced fragment |
Largest integer not greater than x |
|
isnan( x ) |
Advanced vertex and fragment |
True if x is not a number (NaN) |
|
lerp( a, b, f ) |
All |
Linear interpolation between a and b based on f |
|
log2( x ) |
Vertex, advanced fragment |
Base 2 logarithm of x |
|
max( a, b ) |
All |
Maximum of a and b |
|
mul( M, N ) mul( M, v ) mul( v, M ) |
Vertex, advanced fragment |
Matrix-by-matrix multiplication Matrix-by-vector multiplication Vector-by-matrix multiplication |
|
pow( x, y ) |
Vertex, advanced fragment |
Raise x to the power y |
|
radians( x ) |
Vertex, advanced fragment |
Degrees-to-radians conversion |
|
reflect( v, n ) |
Vertex, advanced fragment |
Reflection vector of entering ray v and normal vector n |
|
round( x ) |
Vertex, advanced fragment |
Round x to nearest integer |
|
rsqrt( x ) |
Vertex, advanced fragment |
Reciprocal square root |
|
tex2D(sampler, x ) |
Fragment, restricted for basic |
2D texture lookup |
|
tex3Dproj(sampler, x ) |
Fragment, restricted for basic |
Projective 3D texture lookup |
|
texCUBE(sampler, x ) |
Fragment, restricted for basic |
Cube-map texture lookup |
Function Overloading
The Cg Standard Library "overloads" most of its routines so that the same routine works for multiple data types. As in C++, function overloading provides multiple implementations for a routine by using a single name and differently typed parameters.
Overloading is very convenient. It means you can use a function, for example abs , with a scalar parameter, a two-component parameter, a three-component parameter, or a four-component parameter. In each case, Cg "calls" the appropriate version of the absolute value function:
float4 a4 = float4(0.4, -1.2, 0.3, 0.2); float2 b2 = float2(-0.3, 0.9); float4 a4abs = abs(a4); float2 b2abs = abs(b2);
The code fragment calls the abs routine twice. In the first instance, abs accepts a four-component vector. In the second instance, abs accepts a two-component vector. The compiler automatically calls the appropriate version of abs , based on the parameters passed to the routine. The extensive use of function overloading in the Cg Standard Library means you do not need to think about what routine to call for a given-size vector or other parameter. Cg automatically picks the appropriate implementation of the routine you name.
Function overloading is not limited to the Cg Standard Library. Additionally, you can write your own internal functions with function overloading.
Function overloading in Cg can even apply to different implementations of the same routine name for different profiles. For example, an advanced vertex profile for a new GPU may have special instructions to compute the trigonometric sine and cosine functions. A basic vertex profile for older GPUs may lack that special instruction. However, you may be able to approximate sine or cosine with a sequence of supported vertex instructions, although with less accuracy. You could write two functions and specify that each require a particular profile.
Cg's support for profile-dependent overloading helps you isolate profile-dependent limitations in your Cg programs to helper functions. The Cg Toolkit User's Manual: A Developer's Guide to Programmable Graphics has more information about profile-dependent overloading.
The Cg Standard Library's Efficiency and Precision
Whenever possible, use the Cg Standard Library to do math or other operations it supports. The Cg Standard Library functions are as efficient and precise as—or more efficient and precise than—similar functions you might write yourself.
For example, the dot function computes the dot product of two vectors. You might write a dot product function yourself, such as this one:
float myDot(float3 a, float3 b)
{
return a[0]*b[0] + a[1]*b[1] + a[2]*b[2];
}
This is the same math that the dot function implements. However, the dot function maps to a special GPU instruction, so the dot product provided by the Cg Standard Library is very likely to be faster and more accurate than the myDot routine.
3.3.4 2D Twisting
In the next example you will put expressions, operators, and the Cg Standard Library to work. This example demonstrates how to twist 2D geometry. The farther a vertex is from the center of the window, the more the vertex program rotates the vertex around the center of the window.
The C3E4v_twist program shown in Example 3-4 demonstrates scalar-by-vector multiplication, scalar addition and multiplication, scalar negation, the length Standard Library routine, and the sincos Standard Library routine.
Example 3-4. The C3E4v_twist Vertex Program
struct C3E4_Output {
float4 position : POSITION;
float4 color : COLOR;
};
C3E4_Output C3E4v_twist(float2 position : POSITION,
float4 color : COLOR,
uniform float twisting)
{
C3E4_Output OUT;
float angle = twisting * length(position);
float cosLength, sinLength;
sincos(angle, sinLength, cosLength);
OUT.position[0] = cosLength * position[0] +
-sinLength * position[1];
OUT.position[1] = sinLength * position[0] +
cosLength * position[1];
OUT.position[2] = 0;
OUT.position[3] = 1;
OUT.color = color;
return OUT;
}
The C3E4v_twist program inputs the vertex position and color as varying parameters and a uniform scalar twisting scale factor. Figure 3-4 shows the example with various amounts of twisting.
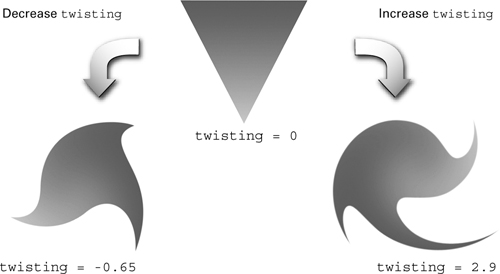
Figure 3-4 Results with Different Parameter Settings
The length and sincos Standard Library Routines
The length routine has an overloaded prototype, where SCALAR is any scalar data type and VECTOR is a vector of the same scalar data type as SCALAR with one, two, three, or four components:
SCALAR length(VECTOR x);
The Cg Standard Library routine length returns the scalar length of its single input parameter:
float angle = twisting * length(position);
The program computes an angle in radians that is the twisting parameter times the length of the input position. Then the sincos Standard Library routine computes the sine and cosine of this angle.
The sincos routine has the following overloaded prototype, where SCALAR is any scalar data type:
void sincos(SCALAR angle, out SCALAR s, out SCALAR c);
When sincos returns, Cg updates the calling parameters s and c with the sine and cosine, respectively, of the angle parameter (assumed to be in radians).
Call-by-Result Parameter Passing
An out qualifier indicates that when the routine returns, Cg must assign the final value of a formal parameter qualified by out to its corresponding caller parameter. Initially, the value of an out parameter is undefined. This convention is known as call-by-result (or copy-out) parameter passing.
C has no similar parameter-passing convention. C++ allows a reference parameter to function (indicated by & prefixed to formal parameters), but this is a call-by-reference parameter-passing convention, not Cg's call-by-result convention.
Cg also provides the in and inout keywords. The in type qualifier indicates that Cg passes the parameter by value, effectively call-by-value. The calling routine's parameter value initializes the corresponding formal parameter of the routine called. When a routine with in -qualified parameters returns, Cg discards the values of these parameters unless the parameter is also out -qualified.
C uses the copy-by-value parameter-passing convention for all parameters. C++ uses copy-by-value for all parameters, except those passed by reference.
The inout type qualifier (or the in and out type qualifiers that are specified for a single parameter) combine call-by-value with call-by-result (otherwise known as call-by-value-result or copy-in-copy-out).
The in qualifier is optional because if you do not specify an in , out , or inout qualifier, the in qualifier is assumed.
You can use out and inout parameters and still return a conventional return value.
Rotating Vertices
Once the program has computed the sine and cosine of the angle of rotation for the vertex, it applies a rotation transformation. Equation 3-1 expresses 2D rotation.
Equation 3-1 2D Rotation

The following code fragment implements this equation. In Chapter 4, you will learn how to express this type of matrix math more succinctly and efficiently, but for now we'll implement the math the straightforward way:
OUT.position[0] = cosLength * position[0] +
-sinLength * position[1];
OUT.position[1] = sinLength * position[0] +
cosLength * position[1];
The Importance of Tessellation for Vertex Programs
The C3E4v_twist program works by rotating vertices around the center of the image. As the magnitude of the twist rotation increases, an object may require more vertices—thus higher tessellation—to reproduce the twisting effect reasonably.
Generally, when a vertex program involves nonlinear computations, such as the trigonometric functions in this example, sufficient tessellation is required for acceptable results. This is because the values of the vertices are interpolated linearly by the rasterizer as it creates fragments. If there is insufficient tessellation, the vertex program may reveal the tessellated nature of the underlying geometry. Figure 3-5 shows how increasing the amount of tessellation improves the twisted appearance of the C3E4v_twist example.
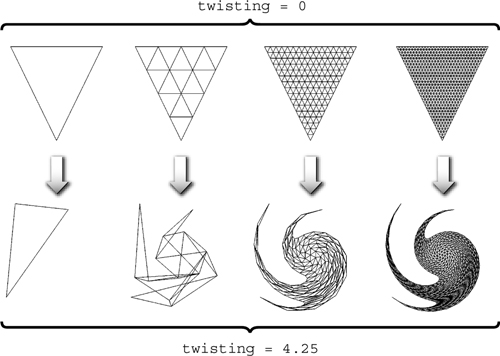
Figure 3-5 Improving the Fidelity of by Increasing Tessellation
3.3.5 Double Vision
Now we demonstrate how to combine a vertex program and a fragment program to achieve a textured "double vision" effect. The idea is to sample the same texture twice, based on slightly shifted texture coordinates, and then blend the samples equally.
The C3E5v_twoTextures vertex program shown in Example 3-5 shifts a single texture coordinate position twice, using two distinct offsets to generate two slightly separated texture coordinate sets. The fragment program then accesses a texture image at the two offset locations and equally blends the two texture results. Figure 3-6 shows the rendering results and the required inputs.
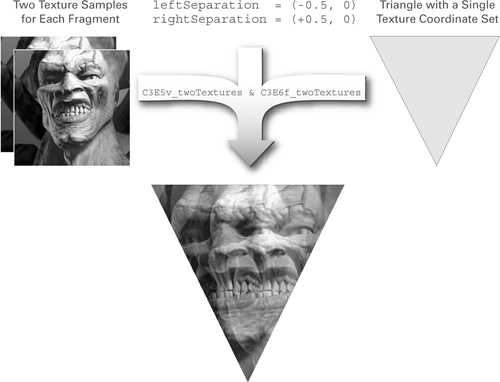
Figure 3-6 Creating a Double Vision Effect with and
Example 3-5. The C3E5v_twoTextures Vertex Program
void C3E5v_twoTextures(float2 position : POSITION,
float2 texCoord : TEXCOORD0,
out
float4 oPosition : POSITION,
out
float2 leftTexCoord : TEXCOORD0,
out
float2 rightTexCoord : TEXCOORD1,
uniform
float2 leftSeparation,
uniform
float2 rightSeparation)
{
oPosition = float4(position, 0, 1);
leftTexCoord = texCoord + leftSeparation;
rightTexCoord = texCoord + rightSeparation;
}
The Double Vision Vertex Program
The C3E5v_twoTextures program in Example 3-5 passes through the vertex position. The program outputs the single input texture coordinate twice, once shifted by the leftSeparation uniform parameter and then shifted by the rightSeparation uniform parameter.
oPosition = float4(position, 0, 1); leftTexCoord = texCoord + leftSeparation; rightTexCoord = texCoord + rightSeparation;
Out Parameters vs. Output Structures
The C3E5v_twoTextures example also shows a different approach to outputting parameters. Rather than return an output structure, as all our previous examples have done, the C3E5v_twoTextures example returns nothing; the function's return type is void . Instead, out parameters with associated semantics, which are part of the entry function's prototype, indicate which parameters are output parameters. The choice of using out parameters or an output return structure to output parameters from an entry function is up to you. There is no functional difference between the two approaches. You can even mix them.
The remainder of this book uses the out parameter approach, because it avoids having to specify output structures. We add an " o " prefix for out parameters to distinguish input and output parameters that would otherwise have the same name—for example, the position and oPosition parameters.
Example 3-6. The C3E6f_twoTextures Fragment Program
void C3E6f_twoTextures(float2 leftTexCoord : TEXCOORD0,
float2 rightTexCoord : TEXCOORD1,
out float4 color : COLOR,
uniform sampler2D decal)
{
float4 leftColor = tex2D(decal, leftTexCoord);
float4 rightColor = tex2D(decal, rightTexCoord);
color = lerp(leftColor, rightColor, 0.5);
}
In Example 3-5 and subsequent examples, we also line up and group the parameters to the entry function as input, output, and uniform parameters. This style takes extra work to format code, but we use it in this book to make the examples easier to read, particularly when the examples have many parameters.
The Double Vision Fragment Program for Advanced Fragment Profiles
The C3E6f_twoTextures fragment program in Example 3-6 takes the two shifted and interpolated texture coordinate sets computed by C3E5v_twoTextures and uses them to sample the same texture image twice, as shown in Figure 3-6.
float4 leftColor = tex2D(decal, leftTexCoord); float4 rightColor = tex2D(decal, rightTexCoord);
Then the program computes the average of the two color samples:
color = lerp(leftColor, rightColor, 0.5);
The lerp routine computes a weighted linear interpolation of two same-sized vectors. The mnemonic lerp stands for "linear interpolation." The routine has an overloaded prototype in which VECTOR is a vector with one, two, three, or four components and TYPE is a scalar or vector with the same number of components and element types as VECTOR :
VECTOR lerp(VECTOR a, VECTOR b, TYPE weight);
The lerp routine computes:
|
result =(1-weight)xa + weight xb |
A weight of 0.5 gives a uniform average. There is no requirement that the weight be within the 0 to 1 range.
Unfortunately, the C3E6f_twoTextures fragment program will not compile with basic fragment profiles such as fp20 and ps_1_1 (you will learn why shortly). It compiles fine, however, with advanced fragment profiles, such as fp30 and ps_2_0 .
The Double Vision Fragment Program for Basic Fragment Profiles
The C3E6f_twoTextures example uses two texture coordinate sets, 0 and 1, to access texture unit 0. Because of this, the program does not compile with basic fragment program profiles. Such profiles can use only a given texture coordinate set with the set's corresponding texture unit due to limitations in third-generation and earlier GPUs.
You can alter the C3E6f_twoTextures program slightly so that it works with basic and advanced fragment profiles. The C3E7f_twoTextures version in Example 3-7 contains the necessary alterations.
Example 3-7. The C3E7f_twoTextures Fragment Program
void C3E7f_twoTextures(float2 leftTexCoord : TEXCOORD0,
float2 rightTexCoord : TEXCOORD1,
out float4 color : COLOR,
uniform sampler2D decal0,
uniform sampler2D decal1)
{
float4 leftColor = tex2D(decal0, leftTexCoord);
float4 rightColor = tex2D(decal1, rightTexCoord);
color = lerp(leftColor, rightColor, 0.5);
}
The modified program requires two texture units:
uniform sampler2D decal0,
uniform sampler2D decal1
So that the two texture units sample the same texture image, the C3E7f_twoTextures fragment program requires the application to bind the same texture for two separate texture units. The original C3E6f_twoTextures program did not require the application to bind the texture twice.
When the program samples the two textures, it samples each texture unit with its corresponding texture coordinate set, as required by basic fragment program profiles:
float4 leftColor = tex2D(decal0, leftTexCoord); float4 rightColor = tex2D(decal1, rightTexCoord);
The performance of these two approaches is comparable. This example demonstrates that simpler Cg programs—those that are not too complicated—can often be written with a little extra care to run on older GPUs, which support basic vertex and fragment profiles, as well as on recent GPUs, which support advanced profiles.
3.4 Exercises
-
Answer this: Beyond mere convenience, why do you suppose the sincos Standard Library routine returns both the sine and the cosine of an angle? Hint: Think trigonometric identities.
-
Answer this: Explain in your own words why the increased tessellation shown in Figure 3-5 is required for the twisted triangle to look good.
-
Try this yourself: Modify the C3E4v_twist example so that the twisting centers on some arbitrary 2D point specified as a uniform float2 parameter, rather than on the origin (0, 0).
-
Try this yourself: Modify the C3E5v_twoTextures and C3E7f_twoTextures programs to provide "quadruple vision." Make sure your new program works on both basic and advanced profiles. Assume that your GPU supports four texture units.
-
Try this yourself: Modify the C3E5v_twoTextures example to return an output structure rather than use out parameters. Also, modify an earlier example, such as C3E4v_twist, to use out parameters rather than return an output structure. Which approach do you prefer?
3.5 Further Reading
You can learn more about 2x2 matrices, such as the rotation matrix in the twist example, in The Geometry Toolbox for Graphics and Modeling (A. K. Peters, 1998), by Gerald Farin and Dianne Hansford.
Copyright
Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed with initial capital letters or in all capitals.
The authors and publisher have taken care in the preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein.
The publisher offers discounts on this book when ordered in quantity for bulk purchases and special sales. For more information, please contact:
U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com
For sales outside of the U.S., please contact:
International Sales
international@pearsontechgroup.com
Visit Addison-Wesley on the Web: www.awprofessional.com
Library of Congress Control Number: 2002117794
Copyright © 2003 by NVIDIA Corporation
Cover image © 2003 by NVIDIA Corporation
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. Published simultaneously in Canada.
For information on obtaining permission for use of material from this work, please submit a written request to:
Pearson Education, Inc.
Rights and Contracts Department
75 Arlington Street, Suite 300
Boston, MA 02116
Fax: (617) 848-7047
Text printed on recycled paper at RR Donnelley Crawfordsville in Crawfordsville, Indiana.
8 9 10111213 DOC 09 08 07
8th Printing, November 2007
Developer News Homepage

Developer Login
Become a
Registered Developer

Developer Tools
Documentation
DirectX
OpenGL
GPU Computing
Handheld
Events Calendar

Newsletter Sign-Up
Drivers
Jobs (1)
Contact
Legal Information

Site Feedback
- Copyright, Dedications and Foreword
- Chapter 1. Introduction
- Chapter 2. The Simplest Programs
- Chapter 3. Parameters, Textures, and Expressions
- Chapter 4. Transformations
- Chapter 5. Lighting
- Chapter 6. Animation
- Chapter 7. Environment Mapping Techniques
- Chapter 8. Bump Mapping
- Chapter 9. Advanced Topics
- Chapter 10. Profiles and Performance
- Appendix A. Getting Started with Cg
- Appendix B. The Cg Runtime
- Appendix C. The CgFX File Format
- Appendix D. Cg Keywords
- Appendix E. Cg Standard Library Functions
- Color Plates